SoftSec Lab 博弈论及应用 更新时间：2024.09.05 21:00 课程QQ群：697295926
实验项目     实验报告模板下载(docx) ⇑⇑
  1. 设计性（1-3周） ⇑⇑
    实验项目
    实验1：博弈智能体设计
    实验目的
    能运用机器学习和人工智能方法设计博弈智能体，使其能够参与博弈模型的自动求解。
    实验要求
    1. 编程实现对酒吧博弈的模拟。
    2. 小镇居民的决策行为通过实现简单的智能体来模拟。
    3. 输出图表，展示模拟效果（一年内去酒吧人数，居民的平均幸福度等）。
    4. 分析结果，得出结论。
    5. 撰写设计说明书（包括程序的设计细节）写入实验报告。
    6. 将程序运行效果截图，粘贴到实验报告中。
    7. 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验1-学号-姓名.zip”。
    8. 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验1-学号-姓名.pdf”。
    9. 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
  2. 设计性（1-3周） ⇑⇑
    实验项目
    实验2：博弈模型自动分析工具设计
    实验目的
    学习用计算机程序实现博弈模型，能设计博弈矩阵分析器和博弈树分析器。
    实验要求
    • 编程实现一个博弈模型的分析器，既能分析博弈矩阵，也能分析博弈树。
    • 输入任意策略式博弈的博弈要素，分析器能够自动生成博弈矩阵，并图形化显示。
    • 输入任意扩展式博弈的博弈要素，分析器能够自动生成博弈树，并图形化显示。
    • 分析器能够根据生成的博弈矩阵或博弈树，列出每个博弈参与者（局中人）的策略集。
    • 分析器能够根据每个博弈参与者的策略集，生成所有策略组合。
    • 分析器能够根据生成的策略组合，得出所有可能的均衡。
    • 撰写设计说明书（包括程序的设计细节和分析器的操作说明）写入实验报告。
    • 将分析器各功能的运行效果截图，粘贴到实验报告中。
    • 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验2-学号-姓名.zip”。
    • 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验2-学号-姓名.pdf”。
    • 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
  3. 设计性（1-2.5周） ⇑⇑
    实验项目
    实验3：经典连续得益无限策略博弈模型的设计
    实验目的
    通过计算机程序和数据分析来验证经典连续得益无限策略博弈模型的正确性。
    实验要求
    1. 选择古诺模型或伯川德模型之一，作为验证对象。
    2. 详细描述一个使用所选模型的博弈场景，给出各博弈要素的完整假设。
    3. 计算所描述博弈场景的纳什均衡，并分析：是否存在其他帕累托效率意义上的上策？为什么没能在该策略组合上达成均衡？
    4. 编写计算机程序，实现两个能够给出策略选择的智能体（对象）来模拟博弈模型中的参与者。
    5. 智能体输入参数的值可以根据上一次博弈的结果进行修正，进而给出新的策略选择，以此模拟博弈参与者根据经验变换策略选择的效果。
    6. 收集并存储每次博弈的过程和结果数据（博弈次数根据需要设定，通常一个收敛的博弈模型，博弈次数越多，实验效果越精细）。
    7. 将博弈的结果数据进行整理，并绘制为折线图（或其他用于数值比较的图表），进而分析双方的博弈结果是否符合所选模型理论上的均衡计算。
    8. 撰写设计说明书（包括程序的设计细节和操作说明等）写入实验报告。
    9. 将验证实验的详细运行效果截图，粘贴到实验报告中。
    10. 将验证实验的结果折线图，粘贴到实验报告中，用来证明博弈模型的正确性。
    11. 注意：由于古诺模型和伯川德模型中的参数应根据具体博弈场景来设定，所以博弈模型不是唯一的，博弈场景也不是唯一的， 每位同学的实验内容和程序应当完全不同，若雷同则不能获得成绩。此外，验证结果正确性的高低将作为实验考核的一个指标。
    12. 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验3-学号-姓名.zip”。
    13. 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验3-学号-姓名.pdf”。
    14. 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
  4. 设计性（1-2.5周） ⇑⇑
    实验项目
    实验4：讨价还价博弈模型的设计
    实验目的
    通过计算机程序和数据分析来验证讨价还价博弈中折现因子对博弈的各方面影响
    实验背景
    假设甲乙两同学正在对1000元奖金的分配进行讨价还价。双方互相不知道对方的折现因子（可以相同也可能不同），但都随机在[0.1,0.9]区间取值（取1位小数）。 然后双方开始进行讨价还价博弈，直到一方接受为止。由于双方的折现因子是不互知的，因此多阶段博弈得以进行，双方互相猜测对方的折现因子，并探查对方的“底线”。 当博弈结束后，两名同学各自给出自己对对方折现因子的猜测，并统计各自的得益结果。
    实验要求
    1. 编写计算机程序模拟上述实验过程，实验轮数尽可能多，以便能从实验数据中验证规律。
    2. 收集实验数据，绘制比较图表，并在屏幕上展示。
    3. 通过对博弈模型的计算，先得出理论上折现因子对博弈的各方面影响（对得益的影响，对双方策略选择的影响，对结果的影响等）。
    4. 通过对博弈数据的分析，再验证理论分析的正确性。
    5. 在实验报告中给出详细的分析过程和结论。
    6. 撰写设计说明书（包括程序的设计细节和操作说明等）写入实验报告。
    7. 将验证实验的详细运行效果截图，粘贴到实验报告中。
    8. 将验证实验的数据折线图，粘贴到实验报告中，用来证明理论分析的正确性。
    9. 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验4-学号-姓名.zip”。
    10. 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验4-学号-姓名.pdf”。
    11. 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
  5. 综合性（1-3周） ⇑⇑
    实验项目
    实验5：完全信息博弈的建模
    实验目的
    掌握完全信息博弈的综合性建模方法，熟悉静态博弈与动态博弈交叉出现的博弈场景建模过程
    实验背景
    这是一个囚徒困境的动态版，事情是这样的。两个爆炸案的犯罪嫌疑人被抓获了，警方意外地发现，他们可能是几年前一桩珠宝店爆窃案的在逃疑犯。 为了得到他们的口供，警察想到了使用囚徒困境的方法让他们分别招供。然而，警察也意识到另一个问题，当两个疑犯最终刑满释放后， 坦白的一方有可能会遭到黑社会组织的报复，报复等级从轻到重分为1-4级，而疑犯可以选择对抗和不对抗两种策略。 同时，坦白的一方还可能会遭到沉默一方的报复，假设黑社会组织的报复等级和沉默一方的报复等级恰好相反，即如果黑社会组织报复的太轻， 那么沉默一方为了泄愤，就会报复的较重。由于警察不清楚黑社会组织具体会给出哪个级别的报复，所以只能猜测不同级别报复的可能性， 而疑犯的策略选择要依据不同报复级别对自己产生的影响，这个影响，警察是不清楚的，因此只能给出估计的得益函数。 现在，如果你是警察，要给两个疑犯设定刑期，也就是囚徒困境中坦白和沉默两个策略组合对应的双方得益情况，目标是让至少一个嫌犯选择坦白， 应该如何设定？
    实验要求
    1. 对上述博弈背景进行建模，编程实现一个系统，模拟该博弈过程。
    2. 警察输入“报复-对抗”博弈的得益函数或情况，对报复等级的信念（即概率分布），“坦白-沉默”博弈的得益函数或情况。
    3. 系统分别计算两个阶段中的两个静态博弈的纳什均衡（包括混合策略和纯策略），然后逆向归纳，得到最终动态博弈的均衡解。
    4. 系统输出警察设定的“坦白-沉默”博弈的得益情况是否符合预期，如果符合，且至少有一个嫌犯坦白，则警察获胜，如果不符合，或者最后没有嫌犯选择坦白，则警察失败。
    5. 在实验报告中给出详细的分析过程和结论。
    6. 撰写设计说明书（包括程序的设计细节和操作说明等）写入实验报告。
    7. 将实验的详细运行效果截图，粘贴到实验报告中。
    8. 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验5-学号-姓名.zip”。
    9. 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验5-学号-姓名.pdf”。
    10. 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
    本实验可以提交视频演示，视频格式要求如下：
    1. 分辨率720p以上。
    2. 时长5分钟以内（如果内容较多，可以通过调整视频倍速来压缩）。
    3. 格式只限mp4（如录制为其他格式，需要转换视频格式为mp4）。
    4. 命名要求为：“演示视频-实验5-学号-姓名.mp4”。
    5. 演示内容的配音要按照实验要求逐项说明（先演示符合实验要求的功能，再介绍代码情况，最后总结优缺点）。
  6. 综合性（1-3周） ⇑⇑
    实验项目
    实验6：不完全信息博弈的建模
    实验目的
    通过将刺杀博弈设计为游戏，熟悉完全但不完美信息博弈的均衡求解过程
    游戏过程
    1. 以《教父》中迈克医院救父情节为背景，计算机扮演迈克，人类玩家扮演杀手。
    2. 计算机随机设定“自然”判定迈克是否持枪的概率分布，如持枪可能性和空手可能性各占50%等。此信息对人类玩家不公开。
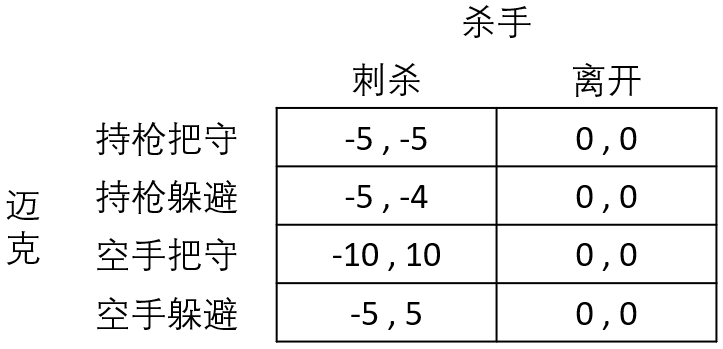
    3. 人类玩家设定双方各种策略组合下的得益情况（任意设定），可参考下表的例子：
      experiment_1
    4. 人类玩家输入杀手对迈克是否持枪的信念，如：
      P(持枪|把守)=2/3，P(空手|把守)=1/3
      P(持枪|躲避)=0，P(空手|躲避)=1
    5. 游戏内部按照“自然”所给出的概率分布来自动确定迈克是否持枪（对人类玩家不公开）。
    6. 第1阶段，计算机按照人类玩家给出的对杀手的信念，用逆向归纳法计算双方的均衡策略，显示迈克的行动并转化为条件概率，如：
      若“自然”确定了迈克持枪，而比较期望得益获知迈克持枪时始终选择把守，则给出“把守”行动，条件概率为：P(把守|持枪)=1，P(躲避|持枪)=0
      若“自然”确定了迈克空手，而比较期望得益获知迈克以混合策略选择行动，则按该混合策略随机给出“把守”或“躲避”，条件概率可能为： P(把守|空手)=1/2，P(躲避|空手)=1/2
    7. 第2阶段，则给出“刺杀”和“离开”两个选项，由人类玩家自由选择。
    8. 计算实际得益，显示双方的胜负。
    9. 游戏内部使用贝叶斯法则验证人类玩家输入的信念是否与后验概率相符（显示比较结果）,
      若不相符，则说明杀手判断失误，即便获胜也是纯属侥幸，可从第4步重新开始一轮新猜测；
      若相符，则可列出双方的完美贝叶斯均衡。
    10. 进阶设计(可选)：调换计算机和人类玩家的角色，由计算机扮演杀手，人类玩家扮演迈克。
    实验要求
    1. 编程实现上述游戏过程。
    2. 撰写设计说明书（包括程序的设计细节和操作说明等），写入实验报告。
    3. 将游戏运行界面截图，粘贴到实验报告中。
    4. 实验源码（必须包含详细可阅读的注释）打包提交，命名为：“实验源码-实验6-学号-姓名.zip”。
    5. 实验报告电子版另存为PDF格式提交，命名为：“实验报告-实验6-学号-姓名.pdf”。
    6. 注意：实验源码和实验报告必须按指定格式命名，并提交指定文件格式的电子资料。
    本实验可以提交视频演示，视频格式要求如下：
    1. 分辨率720p以上。
    2. 时长5分钟以内（如果内容较多，可以通过调整视频倍速来压缩）。
    3. 格式只限mp4（如录制为其他格式，需要转换视频格式为mp4）。
    4. 命名要求为：“演示视频-实验6-学号-姓名.mp4”。
    5. 演示内容的配音要按照实验要求逐项说明（先演示符合实验要求的功能，再介绍代码情况，最后总结优缺点）。